摘要:玻璃配合料均匀度是多因素综合影响的结果,如配合料水分、原料粒级配比、搅拌设备类型、混料时间、加料顺序、原料种类等等。欲探究综合因素的影响结果,必先探究单因素的影响。配合料水分主要受制于原料含水量和制备工序补水量的影响,原料方面又主要是石英砂含水量的影响,这也是配合料水分含量波动的主要原因,并由此波及到配合料制备均匀度的变化。因此,探究配合料水分与均匀度的相关性,对于优化配合料制备工序管制目标、有效提升配合料制备均匀度具有非常重要的意义。
关键词:水分均匀度相关性工序过控
1. 构建数学模型
从配合料水分含量在3.3%~4.9%范围内的均匀度监测数据观察到,配合料均匀度随水分的变化呈现非线性的变化趋势。在实际问题中,从微积分的角度看,不管y变量(均匀度)与x变量(水分)是何种关系,总是可以采用多项式回归模型进行处理的。
1.1构造多项式

1.2递推多项式


为便于计算,以上算法已编入《玻璃配合料管理系统(GBMS-SYSTEM)》,简称GBMS,它不仅涵盖均匀度单因素、多因素的回归分析与指标优化及均匀度核算,还包括配合料粒级级配分析及Redox数分析。
2. 监测配合料数据
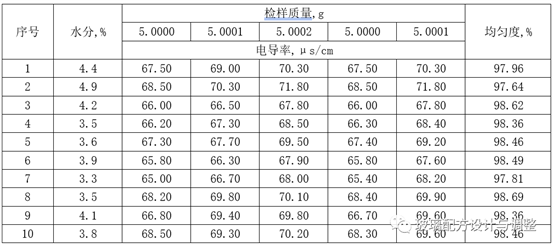
数据分析前首先要获得数据,样本源自某瓶罐玻璃工厂配合料,试验连续取样10天,每次取样点5个分别做电导率检测并进行均匀度核算。同时,从5个样本中分别取部分样混合后用于配合料水分检测,即水分为每日5个样本的平均水分。由此便可获得电导率检测指标50个,均匀度指标10个,水分指标10个,然后进行水分和配合料均匀度的相关性分析。
2.1检测原理
将配合料溶于水,使得配合料中的水溶性盐溶解电离为离子。在这种溶液中插入电极,当电极两极片上加上电压时,则两电极片间的溶液产生电场。在电场的作用下,溶液中的阳离子便移向阴极,阴离子便移向阳极。此时溶液中就会有电流通过,电流的大小与电压成正比,也与溶液的电导率呈正比。因此可以根据各样液的电导率差异来核算配合料均匀度的大小。
2.2检测方法
用天平准确称量5g样本,小心置入300ml烧杯中,加入200ml蒸馏水,用洗瓶洗净粘附烧杯内壁的配合料,擦干杯底水渍及粘附物,放入多头搅拌磁子,置入恒温磁力搅拌器上搅拌5min待测。
打开电导仪电源,归零、校准,然后将电极插入已搅拌好的待检样液中,示值稳定后记录电导率数据(表1),用于均匀度的核算。
表1配合料水分、电导率与均匀度
2.3核算方法
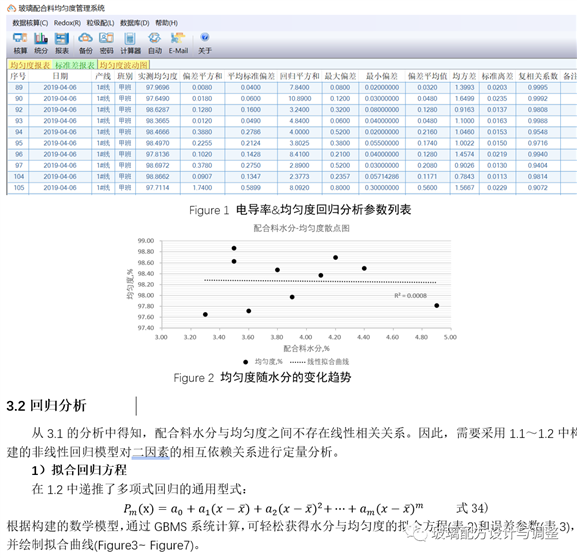
根据电导率核算均匀度的方法通常有极差法和标准差法两种算法。由于配合料属固体物料粒子混合范畴,从统计学角度看,各物料组分的分布是服从正态分布的,因此采用多样本检测、标准差算法是有益于科学地评估配合料制备均匀度的。标准差法均匀度算法如下,计算机软件还可以同步核算导电率与均匀度回归分析的相关参数(Figure2)及均匀度波动曲线。

3. 相关性探究
相关分析用于研究两个随机变量之间是否存在某种依存关系,如配合料水分与配合料均匀度的关系,线性相关的评估模式主要是通过计算相关系数(r)来呈现两个变量间的相关方向以及相关程度,r的取值范围为-1≤r≤1,r的绝对值越接近1,两变量的关联程度越强,r的绝对值越接近0,两变量的关联程度越弱。
线性相关分析侧重于发现随机变量间的种种相关特性,回归分析侧重于探究随机变量间相互依赖的定量关系,是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器)之间的关系,所关心的是一个随机变量(y)对另一个随机变量(x)的依赖关系的函数形式,以便用一个变量(x)去预测另一个变量(y),从而实现工序过控的目的。
本次试验意在通过相关系数模型和多项式回归模型探讨配合料水分与均匀度的相关关系。
3.1相关系数
线性相关程度指标相关系数的表征与核算方法如下:
假设有变量x,y,样本观测值分别为x1,x2,…,xn及y1,y2,…,yn,则两个变量之间相关系数r的计算式为:
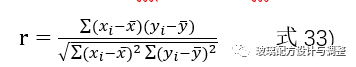
根据式34)~ 式36)即可获得相关系数(r)的计算值。
获得相关系数值后,就需要根据系数进一步评估两个变量间的线性相关程度,相应的判断准则如果:
r>0时为正相关,散点图是斜向上的,这时一个变量增加,另一个变量也增加;
r<0时为负相关,散点图是斜向下的,此时一个变量增加,另一个变量将减少;
|r|=0时不存在线性相关关系;
|r|=1时完全线性相关;
通常情况下,可根据系数大小,做更为细致的评估分类:
|r|≤0.3 不存在线性相关关系;
0.3<|r|≤0.5 低度线性相关;
0.5<|r|≤0.8 中度线性相关;
0.8<|r|≤0.95 高度线性相关;
|r|> 0.95显著线性相关;
本次试验配合料水分与均匀度的相关系数为-0.0283,由此可见,二者之间不存在线性相关关系,散点图示如下(Figure2中①)。但电导率与配合料样本重量之间存高度线性相关关系(Figure1),相关系数高达0.9404~0.9995。
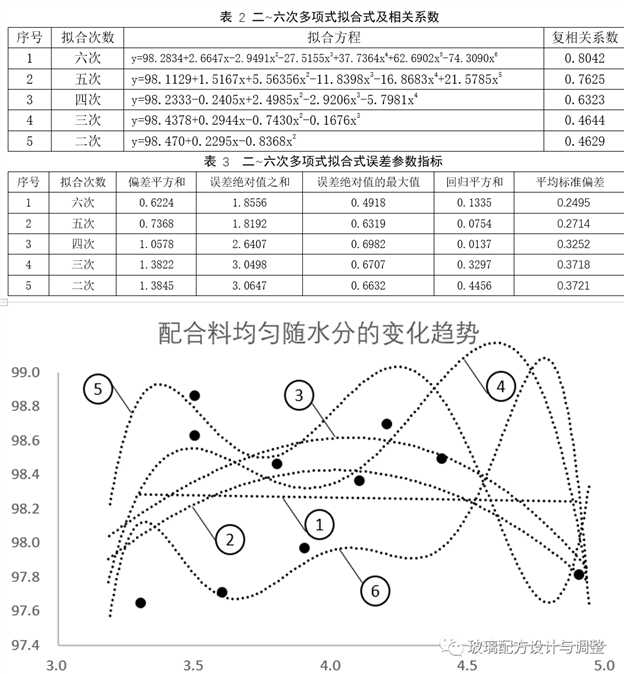
从表2和表3可以看出,随着拟合次数的增加,误差相关参数变化趋势(Figure4)呈现如下变化规律,拟合曲线形态详见Figure3中②~⑥,依次表示二次拟合曲线,三次拟合曲线,…,六次拟合曲线。
复相关系数在逐渐增加;
误差绝对值的极大值先升高然后逐渐降低,在拟合次数4时达到最高,在拟合次数6时最低;
平均标准偏差在逐渐降低;
回归平方和先是降低,四次拟合时达到最低值,然后再逐渐升高;
平均标准偏差,在三次拟合时达到最高,六次拟合时达到最低,总体趋势呈下降趋势;
偏差平方和与平均标准偏差呈现相似的规律性;
误差绝对值之和在五次拟合时达到最低,总体趋势呈现下降趋势;
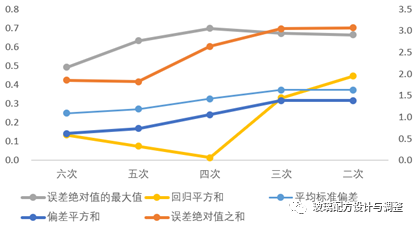
Figure 4回归分析指标随拟合次数升高时的变化趋势
为了预防过拟合现象发生,产生怪异的结果,本次试验选用三次多项式进行显著性分析:
2)显著性分析
回归方程建立后需要通过方差分析评估方程是否符合变量y与x之间的客观规律。
y的总平方和

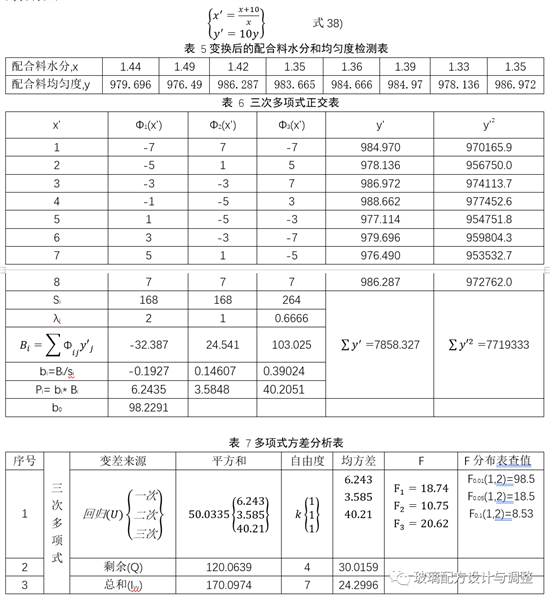
从表7可以看出,F0.1(1,2)=8.53<F1,F0.1(1,2)=8.53<F2,F0.1(1,2)=8.53<F3,即一次、二次、三次多项式在α=0.10水平上都是显著的。
4工序过控中的应用
回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器)之间的关系。通过回归分析,当检验的回归方程为高度显著时,那么它在一定程度上就能客观反映两个变量之间的内在规律。就可以利用回归方程进行工序过控的预测与受控管理,这便是回归分析的工艺学意义。
4.1预测受控范围
预测的含义就是对于给定的x,预测y的散布范围。当x固定于某个特定值时,y是服从正态分布的随机变量,根据正态分布的性质,当x=x0,用y*预测y时,y的实际观测值落在y0±2σ范围内的比例约为95%,落在y0±3σ范围内的比例约为99.7%。因此,σ(标准差)越小,由回归方程预测y的值就越精确。
本次试验中,假设定订均匀度受控值为98%,则根据标准方差与拟合式进行受控线的预测。
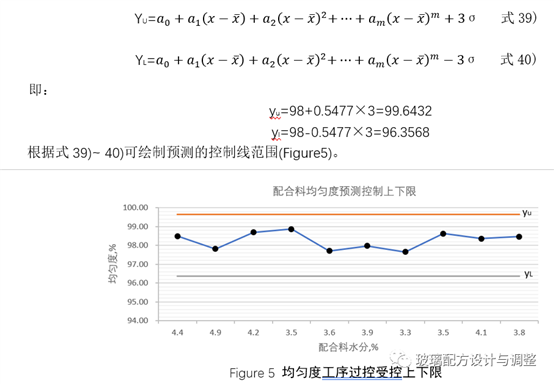
4.2工序可控范围
预测是可预测的可控范围,过程控制则是预测的逆问题,即目标要求y在某范围时,x应该控制的范围,对于本次试验而言,就是先定订均匀度目标受控范围后,如均匀度受控范围95%~98%,再根据均匀度目标要求确定配合料水分的管制范围,并由此开始产线控制和监测。
5.综述
适宜的配合料水分可以润湿砂粒使之形成水膜溶解部分碱金属组分,有益于加速熔化;同时,由于润湿后原料表面粘附性增加,配合料也易于混合均匀,不易分层,还能降低粉尘飞扬,改善操作环境;过高的含水量会降低配合料制备时的温度,对配合料产生胶结作用,阻碍配合料的运动,严重时还容易形成料团,恶化配合料均匀度。
本文探讨了配合料水分在3.3%~4.9%时均匀度的变化情况。当水分含量超过此范围时,这种相关性特性也会随之发生改变,玻璃工厂应当根据实际情况具体问题具体分析。
在配合料的加水过程中,可以同时伴生引入一些降低水分表面张力的原料,这将有益于改善配合料制备品质和熔化品质。
配合料均匀度是多因素综合影响的结果,在探究单因素影响的同时须要关注多因素的综合影响结果,可以借助相关统计手段和计算机软件实现工序过程管制的目的。
参考文献:
[1] 梅长宁,王宁.近代回归分析方法[M].北京:科学出版社. 2012.
[2] 陈乃辉. 统计回归分析[M]. 北京:科学出版社.2012.
[3] 王承遇,陶瑛. 玻璃性质与工艺手册M]. 北京:化学工业出版社.2014.
[4] 王承遇,陈敏.玻璃制造工艺[M]. 北京:化学工业出版社.2006
作者:何旭远